Vector Analysis

How would you size the truss elements of a bridge?

---

---

Using Vectors to Find Forces on Truss Members

In the lesson on Trusses, we built a truss structure out of balsa wood members pinned together into triangular structures. Then, in the lesson on Truss Analysis we found that the reaction forces R₁ and R₂ are each equal to half the applied weight W.

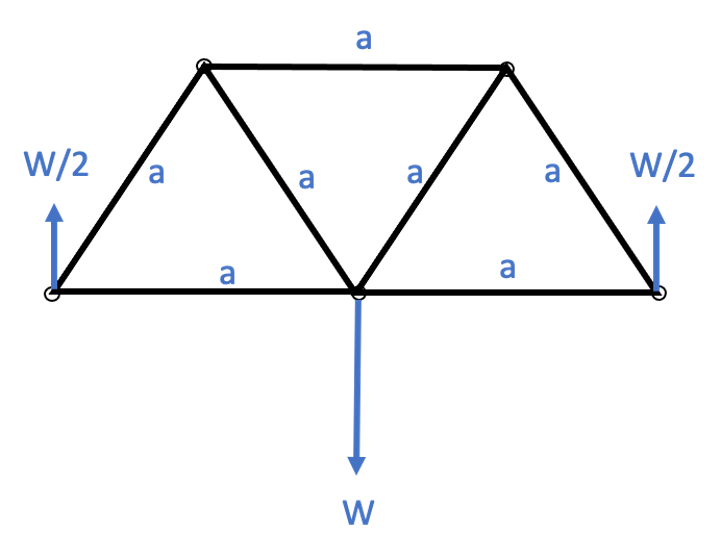
What if we needed to know the forces in each of those balsa wood members?  Perhaps we want to figure out if we’ve opted for thick enough sections of wood to handle the weight we plan to apply, for example.  They key to figuring out these loads are to use vectors!  Recall, vectors have both magnitude and direction; and forces are a vector quantity.  The weight applied is a vector acting downwards.  The reaction forces are vectors acting upwards.  The balsa wood members are helping carry the load – that means there are forces on those members in either tension, pulling on the member, or compression, pushing it together, which can be written as vectors aligned with the members. For example, if I want to solve for the forces in the members on the left-hand side, I can cut an imaginary slice in the truss, shown on the free body diagram below in red, to expose those forces.

Now my diagram looks like this:

I can solve for the forces by writing Newton’s law, that the sum of the forces is zero (the bridge still hasn’t flown away), and by accounting for the vertical direction and horizontal direction separately (the bridge isn’t flying away vertically, nor is it flying away horizontally).  In the vertical direction, I only have two forces on my diagram, W/2 and F₁.  W/2 is entirely vertical, and F₁ is at a 60 degree angle (recall this is an equilateral triangle).  From trigonometry, we can then find the vertical component of F₁ as F₁sin(60).  Summing forces in the vertical direction to find an equilibrium equation gives us:

W/2+F₁sin(60)=0

Which means:

F₁=-(W/2)(1/sin(60))=-W/√3

Wait, so there’s a minus sign there?  That means that instead of pulling on that member, which mean it is in tension, the structure is pushing on that member, so it is in compression! We can now look at all the forces in the horizontal direction to find F₂.  Looking back at our figure, the only forces in the horizontal direction are F₁ and F₂.  Our equilibrium equation in this horizontal direction is:

F₁cos(60)+F₂=0

Since we’ve already solved for F₁ in terms of W, we can solve for F₂ now as:

F₂=-F₁cos(60)=-(-W/√3)(1/2)=W/(2√3)

This is a positive value, so that horizontal member is in tension!  Cool, right, so now I know that if I add 5 Newtons of weight, W, to my bridge at its midpoint, then those two members need to be strong enough to be able to carry:

F₁= _____N

F₂= _____N

With these skills in vectors, geometry, and trigonometry, you can extend this to analyze the complicated trusses you see all around you.

---

Next Steps

Have you gotten to break your truss yet? If not, get out your safety glasses and navigate to the lesson on Gusset Plates.

Or, move on to the unit on Balance to better understand weights and centers for your BLIMP.

---

Last updated: November 23, 2022.