Truss Analysis

How do you design bridge supports to stand the test of time?

---

---

Calculate Reaction Forces

Do you still have the truss that you built in the lesson that first introduced Trusses? If not, take a few minutes to build a new truss like the one pictured below so that you can use it in this exercise.

If you added weight at the bottom center node of the truss, do you know how to calculate the reaction forces (R) at the ends?  If you’re unsure how to do this, start by drawing a free body diagram of your bridge with the weight (W) added.  Then, we can use what we know of forces and moments to solve.  For example, a free body diagram of your bridge, with the added weight, might look something like this, where R₁ and R₂ are reaction forces at the ends, and a is the length of each truss member.  The circles in the diagram are nodes where the members are joined together with pins.

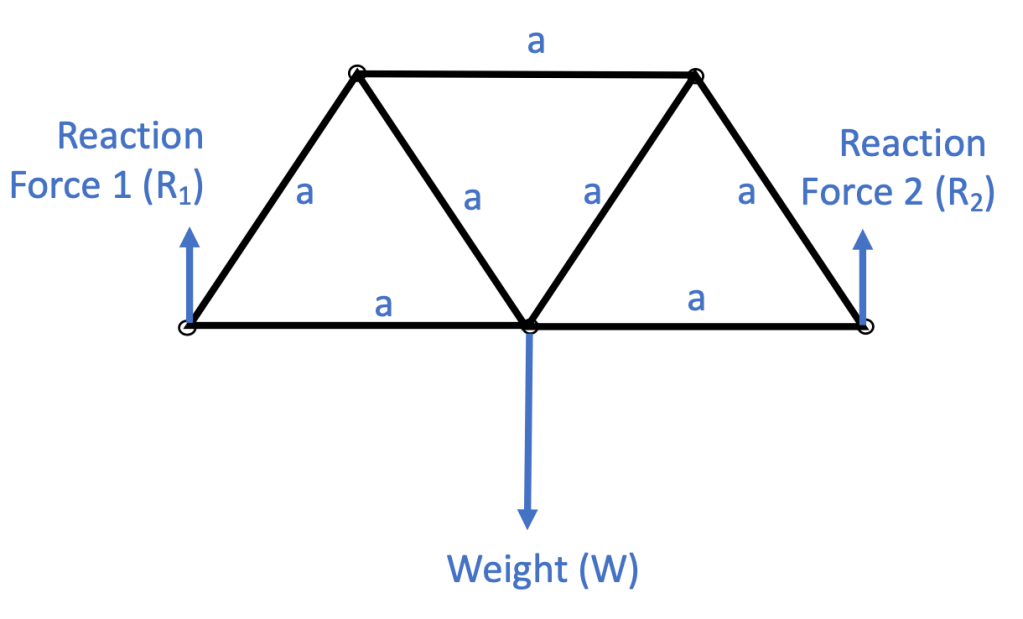
Newton’s second law says the sum of the forces on a body equal’s the body’s mass times its acceleration, but this truss is not flying away, it is static, so the sum of the forces on the truss should equal zero.  Forces are vectors – they have magnitude and direction.  In this case we have three forces, R₁ and R₂ acting upwards and W acting downwards.  So:

R₁+R₂-W=0

That’s great, but we still have two unknown reaction forces, R₁ and R₂.  So, we need a second equation.  Not only is this truss not flying away, it’s not spinning.  We can calculate the moment on the truss from any given force about a specific point by calculating the force multiplied by the distance to the point of interest (the moment arm).  So, let’s take the moment about that central node where the weight is applied.  Because the weight goes right through the node, it has no moment arm, so the moment about that node due to the weight is 0.  But, both R₁ and R₂ cause moments about the node, and because these trusses are built with identical equilateral triangles, R₁ and R₂ both act at equal distances from the central node, although they cause moments in opposite directions.  This can be written mathematically as:

-aR₁+aR₂=0

This equation tells us that R₁ and R₂ must be equal!  Going back to our force balance, that also tells us that both R₁ and R₂ must equal W/2.  Let’s test our math with an experiment!  Prop your bridge up with one end under books and the other end on a scale.  Make sure it’s as close to level as possible; there’s a bubble level in your kit to help with this.  Using the spring balance, pull down on the center node.  Read the value off the spring balance; how much force are you applying?  _______ N

Read the value of the scale at the end; how much force are you measuring?  _______ N  

Was the force at the end ½ what you applied?  

Test your knowledge by repeating the same exercise only now with the force applied halfway between the end and the center.  Draw a free body diagram.  Update the force and moment equations we found previously. based on what you have in your free body diagram.  What do you predict the reaction forces will be?  

Prediction:

R₁=______ N

R₂=______ N

Now re-do the experiment; what do you measure the reaction forces to be?  Note: you can get the reactions at both sides by flipping the location of the scale.

Measurement:

R₁=______ N

R₂=______ N

Did your values agree?  Why or why not?

---

Next Steps

The next step in this process is calculating the forces on individual truss members using Vector Analysis.

If you are looking for a break from analysis work, consider fostering your literary side with Planes, Blimps, and the Aereon 26, or return to the Curriculum to pick your next steps from here.

---

Last updated: November 23, 2022.