Moments of Inertia

Why is it easier to shuffle a deck of cards by bending them along the long axis rather than the short axis?

Learning Objectives

After completing this lesson, the student will be able to calculate moments of inertia for different cross sections.

Standards

  • NGSS HS-ETS1-2
  • CCSS.Math.Practice.MP1
  • CCSS.Math.Practice.MP4

Supplies

  • Ruler
  • Balsa wood sheets
  • Wood glue
  • Knife (see teacher or parent)

Units Used

  • Length: inch (in)
  • Length: centimeter (cm)
  • Length: meter (m)

Moments of Inertia

Let’s do an experiment.  From your balsa wood sheets, cut a rectangle.  I made mine 5 in (12.7 cm) long and 1 in (2.5 cm) wide.  Hold it over the edge of a table with the wide side down, like a miniature diving board, and push on the end.  Then rotate it 90 degrees so the narrow side is down.  Push on the end.  Which way bends more?  Why?

A structure’s moment of inertia (sometimes called the area moment of inertia or second moment of inertia), is a measure of how much a shape resists bending.  For a rectangular cross section, the moment of inertia about its centroidal axis is written as 1/12 bh3, where b is the base of the cross section and h is the height of the cross section.

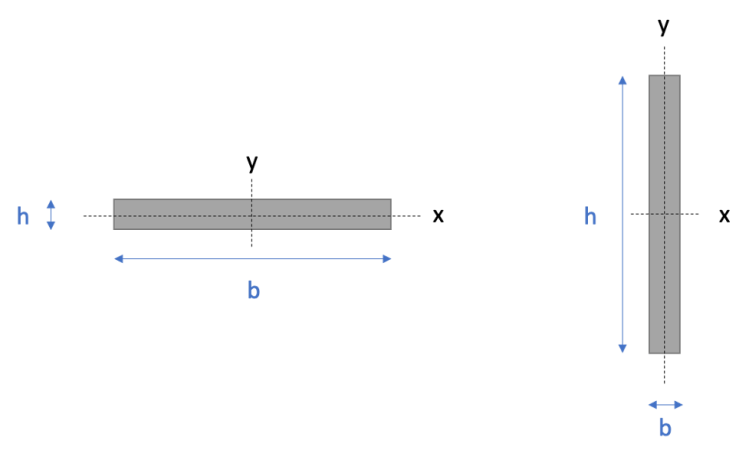
Calculate the moment of inertia for your balsa wood plank in these two orientations.  Which one is larger?  Which one resists bending better?

The real key here is that moment of inertia benefits from having as much area as possible as far as possible from the centroidal axis.  If you have taken calculus, you can see this mathematically by calculating the moment of inertia as Ix=∫y2dA. An experimental way to see this is to build an I-beam.  Cut two more balsawood planks matching the one you made previously, then glue the three planks together to make an I shape.  Repeat your same experiment, hanging the beam off the side of a table and applying a force.  

How did this I-beam fare in comparison to your prior experiments?  Why do you think you had the result you did?

To dig into this more, a nice video tutorial is available at: https://www.youtube.com/watch?v=Bls5KnQOWkY. 

Next Steps

Balance the forces on a BLIMP to set the stage for understanding movement.

A Day in the Life
Form and Function
Balance
Movement
The Literate Engineer

Last updated: November 23, 2022.